Housing – vilemknap.cz

Geographically weighted regression is a multivariate model that is taking into account non-stationarity across space. As the coefficients in GWR may vary across the inspected area, the method is an adequate tool to analyse local properties of the dependent variable.
Comparing with Ordinary least square regression, that generates a single equation for the global model:

(1) $\begin{equation*} \mathbf{Y} = \beta_0 + \boldsymbol{\beta_i} \mathbf{X_i} + \boldsymbol{\epsilon} \end{equation*}$

GWR constructs a separate equation for every feature in the dataset incorporating the dependent and explanatory variables of features falling within the bandwidth of each target feature. The Geographically weighted regression equation is

(2) $\begin{equation*} Y= \beta_0 (u_i,v_i) +\beta_1 (u_i,v_i)x_i1 + \beta_2 (u_i,v_i)x_i2 + ... +\beta_k (u_i,v_i)x_ik + \epsilon_i \end{equation*}$

where (ui, vi) represents the coordinates of the ith point in space. The cordinates for this model are the latitude and longitude coordinates of each polygons‘ centroid. The weight assigned is based on a distance decay function centered at location i and observations nearer to i are given greater weight than observations further away. The (global) ordinary least squares linear regression model assumes that the observations being
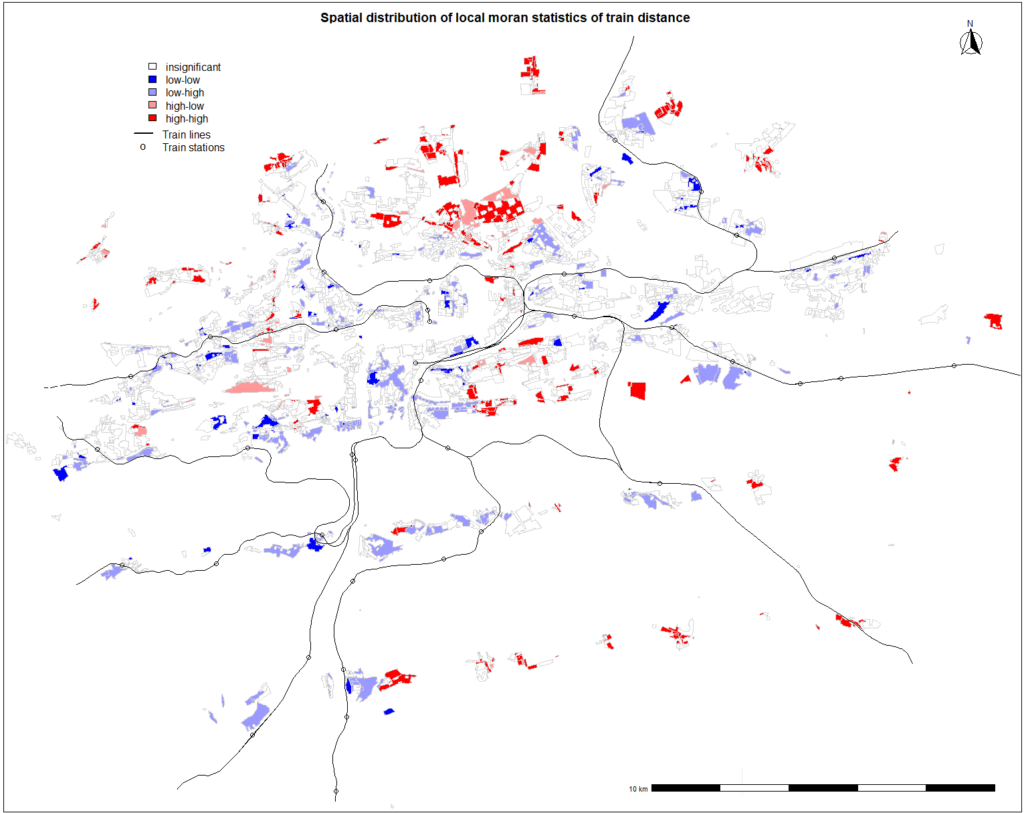
used are independent. As it was already explored in the previous chapter, this assumption is violated as there are significant spatial clustering patterns in the data. In Geographically Weighted Regression, this assumption is relaxed, as it allows for spatially varying coefficients by producing estimates
of the parameter at each data location, factoring in spatial heterogeneity.
Using OLS, the parameters for a linear regression model can be obtained by solving:

(3) $\begin{equation*} \boldsymbol{\beta} = (\mathbf{X}^\intercal \mathbf{X})^{-1} \mathbf{X}^\intercal \mathbf{y} \end{equation*}$

The parameter estimates for GWR may be solved using a weighting scheme:

(4) $\begin{equation*} \boldsymbol{\beta} = (\mathbf{X}^\intercal W(u,v) \mathbf{X})^{-1} \mathbf{X}^\intercal W(u,v) \mathbf{y} \end{equation*}$

The weights are chosen such that those observations near the point in space where the parameter estimates are desired to have more influence on the result than observations further away.
The Gaussian function is used for the weight calculation, the weight for the ith observation is:

(5) $\begin{equation*} w_i = exp (-d_i/h)2 \end{equation*}$

where $d_i$ is the Euclidean distance between the location of observation i and location (u,v), and h is a bandwidth.

Spatial distribution of local Moran statistics for nearest train station distance is illustrated. It can be seen that the train network in Prague is shaped into a star with the main terminal (Praha Hlavní nádraží) in the city center. This corresponds with the original purpose of the system as it was designed to be used as a commuter rail for the suburban regions. There are 10 sections of the train lines that leads to Central Bohemian Region and the majority of low distance regions are aligned around them. Red polygons can be seen in the geographical center of the map however this cluster is completely surrounded by rail lines and it is well connected to other modes. North of the city center, large cluster of red polygons can be observed near Bohnice Municipality. It seems that this clustering pattern is repeating as some of these clustered areas has turned out red for buses and metro distances as well, implying poor connectivity which apparently leads to lower residential land prices in this region, concluding similar results with the findings in empirical analysis.

Štítek: Housing

Geographically Weighted Regression

Spatial distribution of moran statistics for nearest train station distance