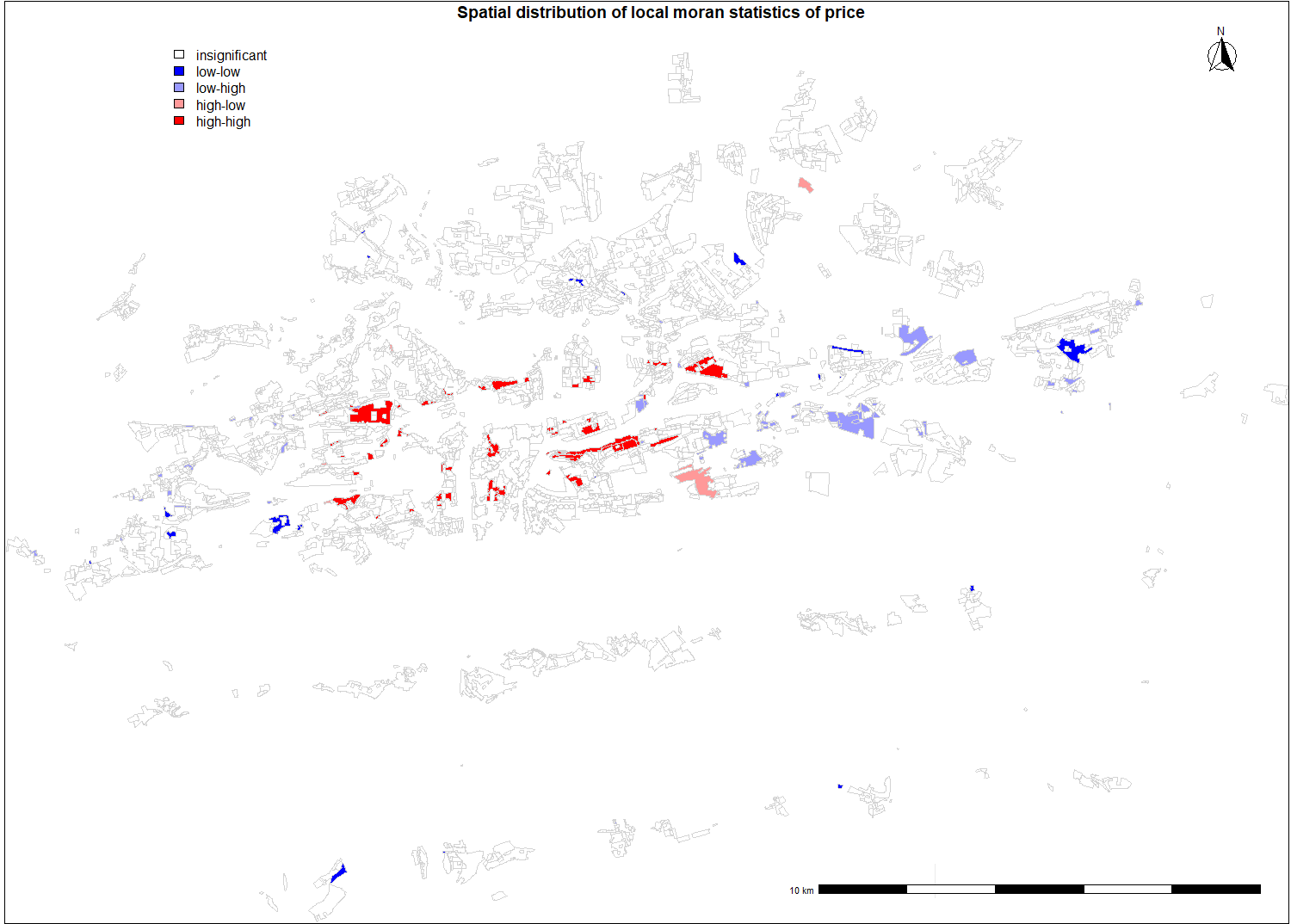
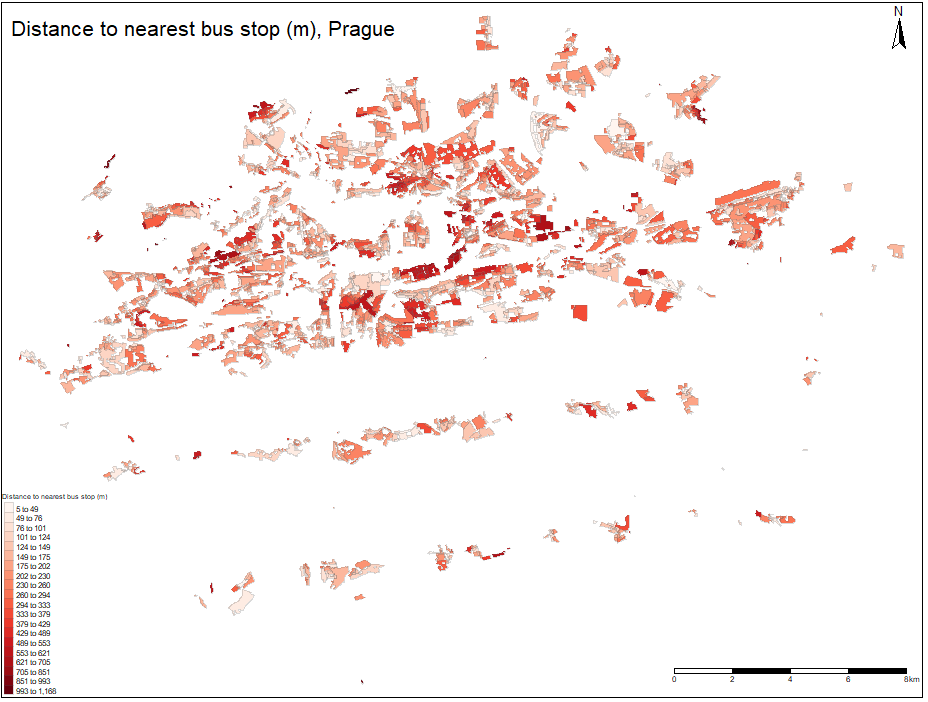
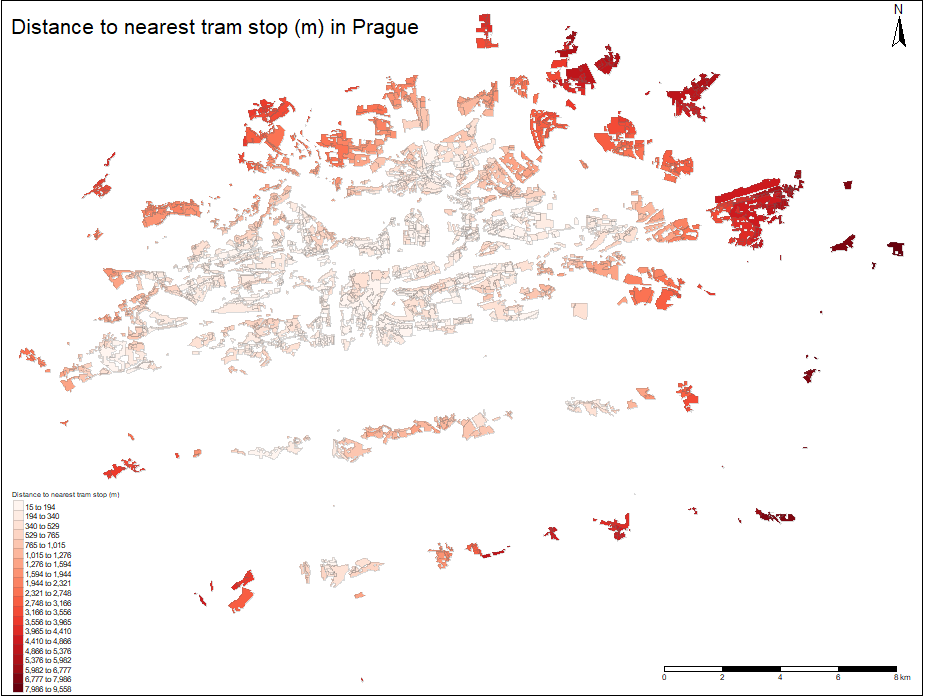
When investigating spatial distribution of local moran statistic of price, we can observe several high value polygons neighbouring with another high value polygons. The most apparent is red area north west. This neighborhood is called Hanspaulka and it consists of historical mansions. Smaller red polygons nearby consists of historical villas as well and they offer beautiful view on the Prague Castle which is nearby. The mentioned factors explain that these areas follow similar spatial clustering pattern. East of the Vltava river meander another large red polygon can be observed. This neighbourhood is called Harfa and it contains newly built luxury penthouses. Generally it can be concluded that high area regions neighbouring with another high area regions consist of either historical mansions, luxury penthouses or historical apartment blocks. Large blue polygons on the eastern part of the city contains mostly separated concrete panel apartment blocks, that were built during communist era. Although the outlying blue polygon on the south end of the city consist of detached houses, its located near highway and ring road crossing and no metro station is nearby, these factors contributes to result of low value of moran statistics.